INTRODUCTION

This e-booklet has been compiled to assist potential owner-builders of Geodesic Domes to prefabricate and erect a variety of geometric configurations utilising a number of possible construction techniques.

Much of the data is gleaned from long-out-of-date publications and from the author’s practical experience and experimentation in building domes since 1973.

Most of the ideas within have been tested and proven successful but are certainly open to further refinement and development. Rather than promoting any one system as being the ‘best’, I would prefer to offer ideas and possibilities to the great Australian tradition of “Do-it -yourself” and share my own experiences of what can work.

With this in mind I welcome any feedback about your own experiments, learning experiences and successes and invite any correspondence to share such knowledge. This manual is intended for educational purposes only.

It presents information on principles and techniques that the author has not necessarily employed. It is not suggested that these methods must be followed or that if followed will result in a safe or satisfactory building.

Due to variations in materials, quality of workmanship, tools and equipment, materials and components, local building codes etc., the author assumes no liability for any structure designed or constructed from information in this manual unless it is built by The Dome Company or our nominated sub-contractor.

 

Geodesic Geometry

GEODESIC = The shortest line between two points on a sphere.

There are only five different structures that we can build where all the sides, faces and angles are equal. These regular solids are called PLATONIC solids.

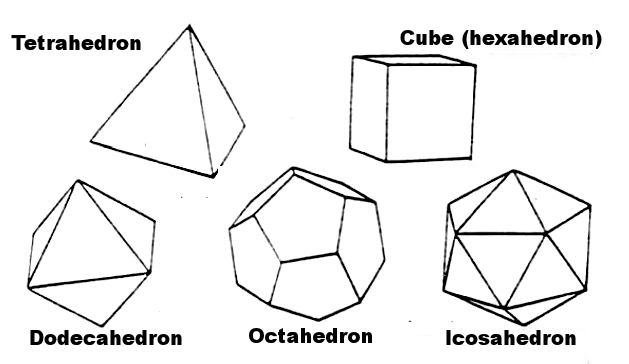
Of these five, we see that three are made of triangles. As we might expect, the tetrahedron,octahedron and icosahedron are rigid; while the cube and dodecahedron are not. The cube is the basis for most types of buildings. The icosahedron is the basis for most Geodesic Domes.

You can make small structures with icosahedrons, but if you begin to make bigger structures, the triangles get large and heavy and you begin to need big timbers for the members.

Dome geometry is all about the subdivision of large triangles into smaller ones.

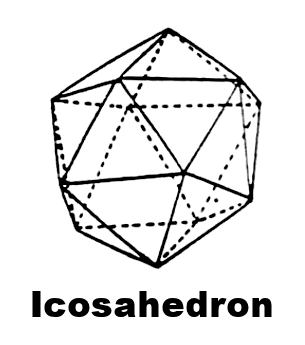An Icosahedron has twenty equilateral triangular ‘faces’. When the face is subdivided. it is not
done equally, but done so that the faces begin to curve outward;this gives you more strength. Each face can be divided by a line (arcs on a sphere) parrallel to the edge.

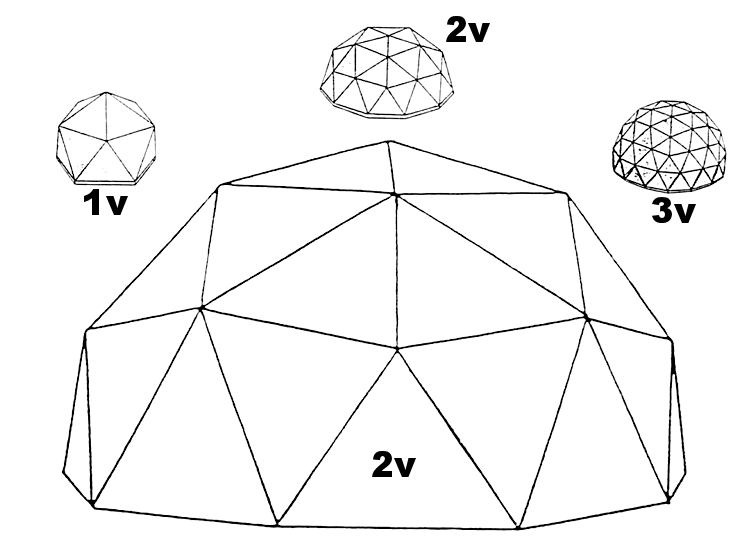
The number of divisions is called “FREQUENCY”.

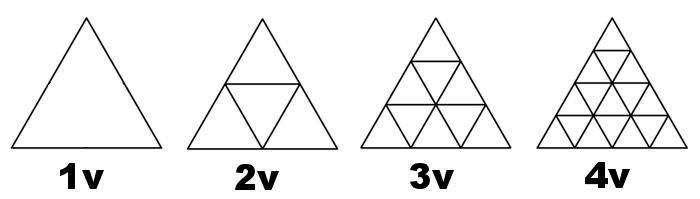
As the frequency increases, the number of members or “STRUTS” and the numbel of triangles increases also, and the closer you get to a sphere.

The following diagram below is of a THREE FREQUENCY (3v) ICOSA 5/8 SPHERE.

Each of the original Icosa faces is heavily outlined. Looking at a geodesic dome on can determine the frequency by counting the number of struts between the apexes 0f the pentagons.

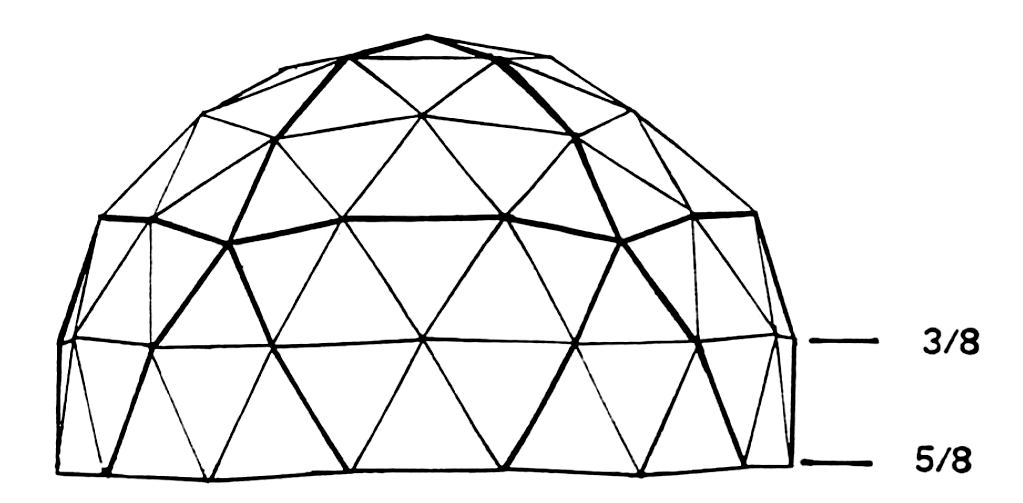
Note: divisions are different for different frequencies. See chart below for correct nomenclature

 

Consider the domes outlined below