MODEL MAKING
By far the best way to see what a geodesic dome looks like is to build three dimensional models. This is not difficult and lets you see how the geometry works, what size and shape you like and possible window and door placements.
The best drawings and photos are inferior to the simplest model when it comes to demonstrating three dimensional relationships.
Playing with models can lead to the discovery of valuable insights; not to mention that they are fun to make and look beautiful too.
There are two basic types of model building, as is full scale dome building. These are:
- The HUB AND STRUT method. ie. Building a framework and then covering it with a skin. and
- The MEMBRANE or PANEL system. ie. Where the skin is attached to the struts in premade triangular panels and the panels are later bolted together.
Before starting your first model, there are a few more simple geometric elements to become familiar with. These are:
CHORD FACTORS, CENTRAL ANGLES, AXIAL ANGLES,
FACE ANGLES and DIHEDRAL ANGLES
For each type of dome there is a method of calculating strut lengths and the angles at which they meet and how they are assembled.
The CHORD FACTORS are of the most importance here as they are needed to determine strut lengths.
Chord Factor = 2 Sin (Central Angle/2)
STRUT LENGTH = DOME_ RADIUS X CHORD FACTOR
Once you have a table of chord factors you can calculate strut length for any size dome you want.
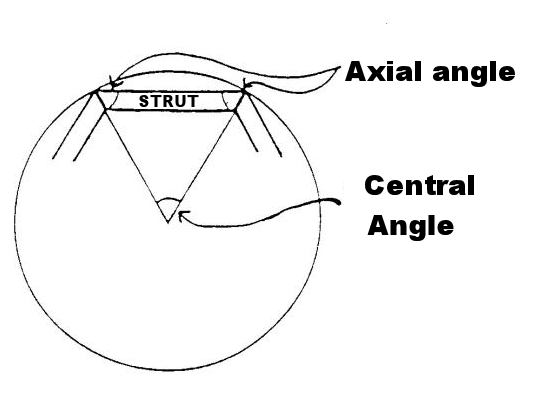The CENTRAL ANGLE is the angle produced by extending a line from the strut ends to the centre of the sphere.
AXIAL ANGLES are useful in hub design. They are the angles that the strut ends make with the centre of the sphere.
Axial Angle = 180 degrees minus Central Angle /2
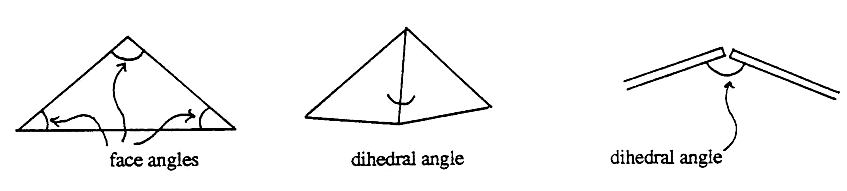
FACE ANGLES are the internal tip angles of the triangles and are necessary when cutting hubs and triangle panels.
DIHEDRAL ANGLES are the angles between triangles. They are useful if you plan to bevel the skin panels or use bevelled struts.
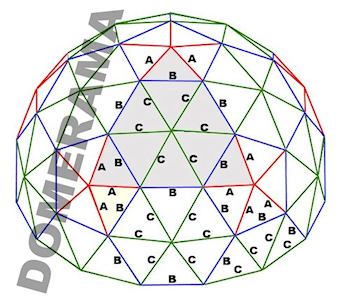
2v and 3v breakdowns with original Icosa face dotted
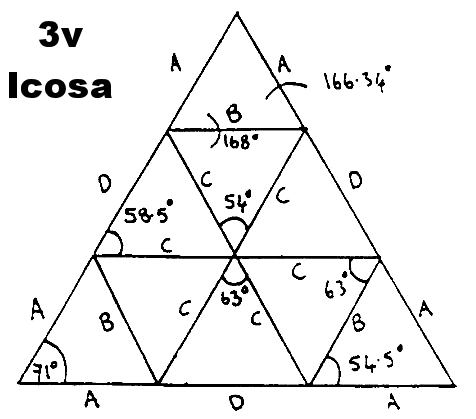
The diagram above shows the statistics for a Three Frequency Icosahedron Dome. To make a 5/8 sphere you will need:
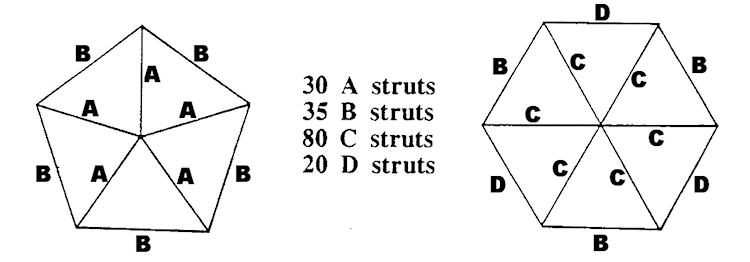
Choose your method of model assembly (following pages) and assemble as in the diagram on page 8. This model will sit ?at on the 3/8 and 5/8 levels. It is simpler to join all the pentagon and hexagon spokes together ?rst. Make six pentagons from “A” struts, ten hexagons from “C” struts and ?ve “halt” hexagons for the base.
A simpler model can be made using only three strut lengths by substituting “D” struts with “B” struts and using the new chord factors of:
A = .34862 need 30
B = .40355 need 55
C = .41241 need 80
This model will not sit flat however but will rest on the five half-hex hubs under the pentagons. For a very similar truncation (fraction of a dome), the Kruschke method is used (in this case a 5/9).
Three-frequency icosahedron spheroid
